Background Reading: How does the reproductive value change over the lifespan?
Mathematically we define reproductive value
where and are the age-specific survivorship and birth rates, respectively. The value is the current age; represents future ages from on to the end of the life span, . The value represents the probability of surviving from age to age in the future. When age is achieved, young are produced. Thus, the sum of for all future ages is the expected number of offspring the individual will produce over the rest of the life span. The logic of this equation is that the relative contribution of an individual is the result of its age-specific survival and birth rate.
All the components of the life history—development, life span, and reproduction—contribute to the value of . Developmental and reproductive patterns have mortality costs. In this way, reproductive value integrates the components of the life history: a change in one component affects others. If there is variation among individuals in the apportionment of energy to various aspects of the life history, the effect will be manifest in the individual’s reproductive value.
For additional background information, please see Section 10.1 of Chapter 10, What is Optimized in the Evolution of the Life History Strategy?
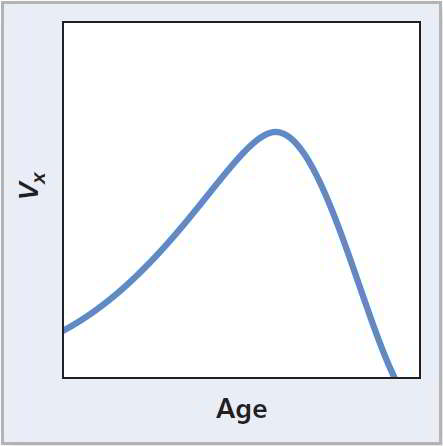
Figure 10.3 The reproductive value, the organism’s age-specific expected reproductive contribution to the next generation, changes with age.